Expected Linear-Time Minimum Spanning Trees
TLDR
- Implemented a complex expected linear time algorithm for finding Minimum Spanning Tree.
- Found a bug in an implementation in a 13 years old paper.
- Code available at github
Context
It was the end of 2019 and I was searching for an interesting topic for my CS undergraduate final thesis. I was looking into randomized algorithms and was really surprised to find out that there was an expected linear time complexity algorithm for the Minimum Spanning Tree problem. The authors are Karger, Klein and Tarjan and from now on I’ll refer to it as \(KKT\), not to be confused with “Karush-Kuhn-Tucker”.
In my algorithms class and also during my studies for the ICPC I had only stumbled upon 3 different ways of solving the problems, with a complexity of \(O(m \cdot \log(n))\) where \(m\) is the number of edges and \(n\) is the number of vertices in the graph
 |
|---|
| Cute Animation of Borůvka algorithm. |
An algorithm with expected complexity of \(O(m + n)\) belongs to a complexity class that grows slower than the class offered by the classical algorithms listed above, so for graphs sufficiently large \(KKT\) algorithm should come in handy. At this point I was super curious to test the performance of it against the classical algorithms.
Let’s benchmark it!
Benchmarks are nice, but there was not going to be easy… As of early 2020, I couldn’t find a working implementation of the \(KKT\) algorithm that I could use for benchmarking purposes.
At this point I had 2 reasonable options:
- Go find some other topic for my undergrad thesis.
- Be brave and implement this not-so-trivial \(KKT\) algorithm and make a publicly available implementation. This can work as a thesis + satisfy my personal curiosity + hopefully contribute a working implementation to society.
As you have probably guessed (given the title of this post), I went for option 2.
When implementing a complex algorithm, how can we find out estimate the implementation complexity?
When we are dealing with a simple algorithm to implement, it is much easier to inspect every small detail of the implementation and become somewhat confident that the implementation actually matches the theoretical complexity. Even in those cases it is not unusual to find out situations where the implementation does not behave as expected, like in the Binary Search Bug.
For more complex algorithms, things get even trickier. My approach was to use the google benchmark project, that fortunately has a complexity “estimation” feature built-in. It was also super convenient to use. It is worth mentioning that this is only an estimate of the implementation complexity and not a guarantee. To see how I used it in the scope of my project, see my benchmarking file.
Hard bug
After completing thinking I had completed the implementation of \(KKT\). It
was natural for me to test my implementation with a rich set of different
graphs. I had ~3 months to complete the tests and write my thesis report
and prepare my presentation.
But there was a catch! I was validating the \(KKT\) result against the minimum spanning trees produced by the other classical algorithms. When testing on graphs with > 1000 nodes, I got an error in about 1% of the instances, in which the solution discovered by \(KKT\) were around 1% worse than the solutions found by all the 3 classical algorithms.
It was something terribly hard to debug, because I couldn’t reproduce the issue with graphs of a smaller size. As someone who has made a lot of implementation mistakes in the past, my usual instict is to assume the error is in some implementation mistake I made. This reminds me of the time when Rafael Nadal played with a broken racket when he was 15, because he was so used to taking responsibility for his losses that the idea that the racket was broken didn’t even cross his mind.
After scrutinizing the code for a long time and adding A LOT of print statements, I started suspecting that the error might not be on me this time. How could that be?
Well, \(KKT\) leverages another complicated algorithm as a fundamental step. This step basically needs to check if a certain tree \(T\) is a minimum spanning tree for a certain graph, which is not something specially hard. The hard part is that needs to have \(O(m + n)\) complexity and that makes the implementation much harder.
It was actually so complicated that it inspired funny paper names:
- Linear Verification For Spanning Trees, 1984 Komlós
- A Simpler Minimum Spanning Tree Verification Algorithm, 1997 King
- An Even Simpler Linear-Time Algorithm for Verifying Minimum Spanning Trees, 2009 Hagerup
I am forever grateful to Hagerup, which is the only author that included his implementation as part of the paper. After a lot of time banging my head against the wall, I was able to find a really subtle typo in the code he provided. A beautiful case of finding the needle in the haystack.
Wrong version from paper:
S = down(D[v], S & (1 << (k + 1) - 1) | (1 << depth[v]));
Corrected version :
S = down(D[v], S & ((1 << (k + 1)) - 1) | (1 << depth[v]));
Fixing this line made my implementation work (at least with my tests).
Ok, but how fast is \(KKT\) anyway?
As I mentioned earlier, I used the google-benchmark code to estimate the runtime complexity of my implementation. Another cool fact is that is also estimates the constants in your implementation.
In Big-\(O\) analysis we ignore constants, but they can make a huge difference in the runtime of your algorithm and how large the instances have to be to make one algorithm “better” than other. You can see my benchmark results here.
Estimated runtime of Borůvka was \(4.67 * N * \log_{2}{N}\) and for \(KKT\) the estimated complexity was \(2357 * N\), where \(N\) here is total edges + nodes in the graph.
So, for sufficiently large \(N\) we expect that \(KKT\) will beat Borůvka. But how large does \(N\) have to be?
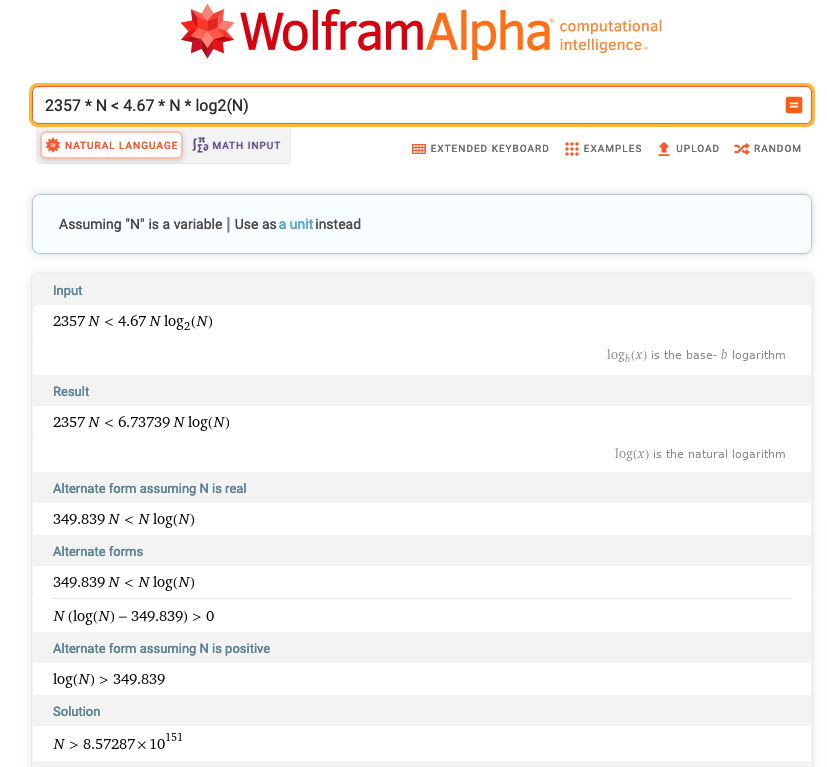
So assuming this equation returned by the benchmark library holds for larger graphs, we would need a graph with \(|Nodes| + |Edges| > 9 * 10^{151}\).
A quick research tells us that:
- Total amount of information accumulated by humanity to date is estimated to be around \(2.95 * 10^{20}\) bytes.
- The number of atoms in the observable universe is estimated to be in the order of \(10 * 10^{82}\).
So not only humanity today is not able to store a graph large enough for my \(KKT\) implementation to beat my Borůvka implementation, but even if the graph had the size equal to the amount of atoms in the observable universe that would not be large enough. There is a name for algorithms like that, they are called Galactic Algorithms (:
Final remarks
- Even though Big-\(O\) analysis ignores constants, they can make a certain algorithm impractical for real world instances.
- It is obviously possible to try to reduce the constant of my \(KKT\) implementation, but I don’t believe it will make the algorithm better than the classical alternatives for real world examples.
- The analysis used estimates of the implementation runtime complexity, this will change if a different set of tests are used for benchmarking.
- At least we now have a publicly available implementation of expected linear time algorithm to finding minimum spanning trees.
- Be aware that when you propose a complicated algorithm, you might cause a student to try to implement it 10/20 years later (:
Credits
I want to thank all the amazing algorithms professors that I had in life, who taught me with great enthusiasm and also offered several suggestions on how to improve my thesis/this blog post.
- Marcus Poggi
- Eduardo Laber
- Marco Molinaro
- Daniel Fleischman
Unanswered questions / additional thoughts
- Is it worth the time trying to reduce the constant of my \(KKT\) implementation? A significant speed-up could make this somewhat useful for really large (but real-world) instances.
- A breakdown of the time spent in each function of \(KKT\) implementation would be interesting to see.
- Is there a class of graphs in which \(KKT\) is more “competitive”?
Relevant links
Suggestions
I am always open to suggestions and/or feedback, if you have something to say please send me an e-mail